728x90
반응형
틱톡라이트 초대링크 https://lite.tiktok.com/t/ZSjqX7SfC/
[기간 한정] 보는 재미로, 버는 재미로! 영상만 봐도, 좋아요만 눌러도, 검색만 해도, 포인트가 차
www.tiktok.com
고득점Kit > 탐욕법(Greedy) > 단속카메라

※ 주의 : 문제풀이 방법은 다양합니다. 참고만 해주세요 ※
[문제설명]
더보기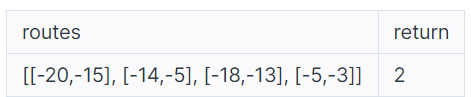
고속도로를 이동하는 모든 차량이 고속도로를 이용하면서 단속용 카메라를 한 번은 만나도록 카메라를 설치하려고 합니다.
고속도로를 이동하는 차량의 경로 routes가 매개변수로 주어질 때, 모든 차량이 한 번은 단속용 카메라를 만나도록 하려면 최소 몇 대의 카메라를 설치해야 하는지를 return 하도록 solution 함수를 완성하세요.
제한사항
- 차량의 대수는 1대 이상 10,000대 이하입니다.
- routes에는 차량의 이동 경로가 포함되어 있으며 routes[i][0]에는 i번째 차량이 고속도로에 진입한 지점, routes[i][1]에는 i번째 차량이 고속도로에서 나간 지점이 적혀 있습니다.
- 차량의 진입/진출 지점에 카메라가 설치되어 있어도 카메라를 만난것으로 간주합니다.
- 차량의 진입 지점, 진출 지점은 -30,000 이상 30,000 이하입니다.
입출력 예

입출력 예 설명
-5 지점에 카메라를 설치하면 두 번째, 네 번째 차량이 카메라를 만납니다.
-15 지점에 카메라를 설치하면 첫 번째, 세 번째 차량이 카메라를 만납니다.
[간단설명]
모든 차량의 이동경로 사이에 감시카메라를 설치할 때, 최소한의 설치 개수 리턴
[접근방법]
1. 리스트를 만들고 배열을 넣는다.
2. 리스트를 진출지점 오름차순 정렬한다.
3. 진출지점을 비교해서 카메라 개수를 증가시킨다.
4. 카메라 개수를 리턴한다.
[주의사항]
1. 이중 루프를 돌면 시간초과가 날 수 있다
2. 진입지점이이 됐든 진출지점이 됐든 1가지만 비교대상으로 선정한다(Greedy 알고리즘)
[소스공개]
import java.util.*;
class Solution {
public int solution(int[][] routes) {
// 정렬용 리스트
List<int[]> list = new ArrayList<>();
// 모든 경로를 리스트에 넣는다
for(int[] r : routes) list.add(r);
// 진출지점으로 오름차순 정렬 (routes[i][1])
// ex) [-20,-15], [-18,-13], [-14,-5], [-5,-3]
Collections.sort(list, (o1,o2)->o1[1]-o2[1]);
// 카메라 개수
int count = 0;
// 진출지점 최소값
int min = -30000;
for(int[] route : list){
// 이전 진출지점이 다음 차량의 진입~진출 범위에 있으면 skip
// ex) [-20,-15], [-18,-13], [-14,-5], [-5,-3]
// 1회차: (min=-30000) -> (min[-30000] < -20 < -15) -> min=-15, counnt++
// 2회차: (min=-15) -> (-18 < min[-15] < -13) -> skip
// 3회차: (min=-15) -> (min[-15] < -14 < -5) -> min=-5, counnt++
// 4회차: (min=-5) -> (-5 <= min[-5] < -3) -> skip
// count=2
if(min>=route[0] && min<=route[1]) continue;
min=route[1];
count++;
}
return count;
}
}
[실행결과]

반응형
'코딩 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/JAVA] 고득점Kit > 탐욕법(Greedy) > 조이스틱 (by 다알쥐AI) (2) | 2024.10.19 |
|---|---|
| [프로그래머스/JAVA] 고득점Kit > 탐욕법(Greedy) > 큰 수 만들기 (by 다알쥐AI) (1) | 2024.10.15 |
| [프로그래머스/JAVA] 고득점Kit > 탐욕법(Greedy) > 체육복 (by 다알쥐AI) (2) | 2024.10.14 |
| [프로그래머스/JAVA] 고득점Kit > 완전탐색 > 모음사전 (by 다알쥐AI) (0) | 2024.10.13 |
| [프로그래머스/JAVA] 고득점Kit > 완전탐색 > 전력망을 둘로 나누기 (by 다알쥐AI) (2) | 2024.10.13 |



